Interview -- 算法

Huy大约 7 分钟

总述算法的一些常见考题和常见数据结构等。

常见数据结构

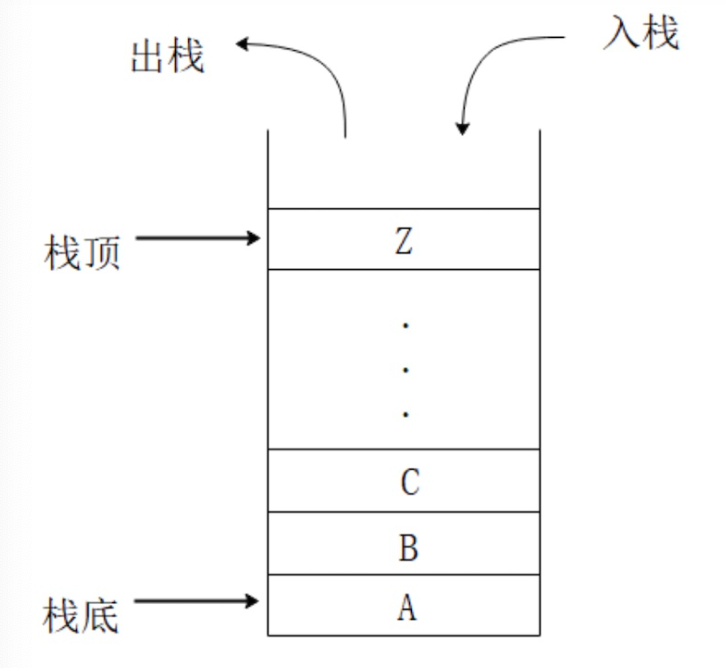
栈 Stack

栈是先进后出的一种数据结构。

const stack = []
stack.push('xxx') // 压栈
stack.pop() // 出栈

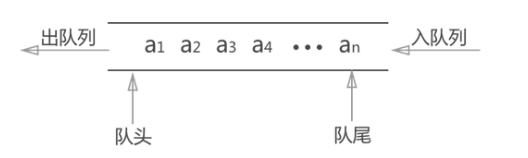
队列 Queue

队列是先进先出的一种数据结构。

const queue = []
queue.push('xxx') // 入队
queue.shift() // 出队

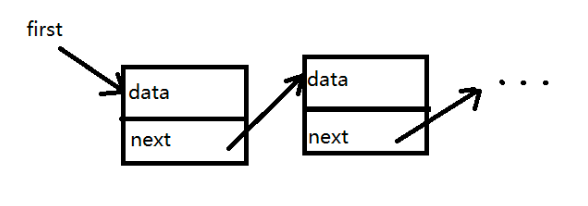
链表 Linked list

链表不是连续的数据结构，而是由一些列的节点组成，各个节点之间通过指针连接。

interface IListNode {
  data: any
  next: IListNode | null
}

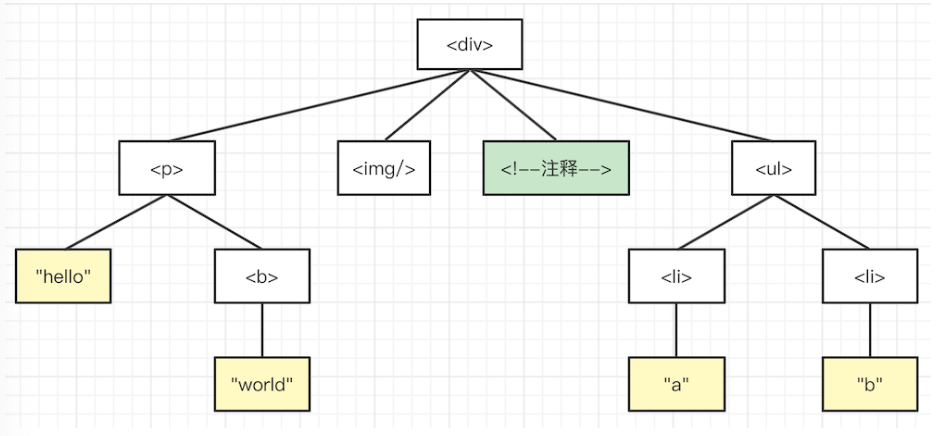
树 Tree

树，是一种有序的层次结构，每个节点下面都可以有若干个子节点。常见的树有 DOM 树。

interface ITreeNode {
  data: any
  children: ITreeNode[] | null
}

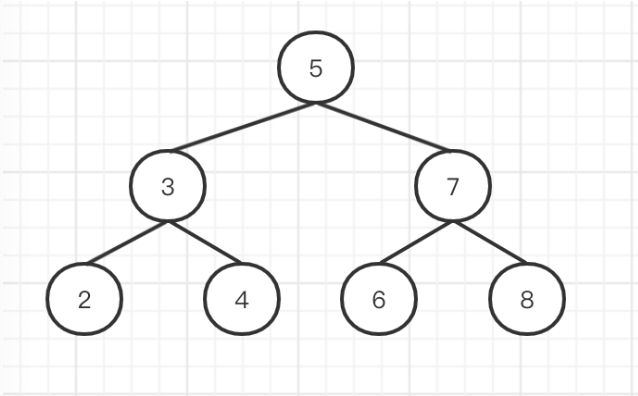
二叉树

二叉树，是树的一种特殊结构，它的每个节点最多只有只有俩个，分别为 left 和 right。

interface IBinaryTreeNode {
  data: any
  left: IBinaryTreeNode | null
  right: IBinaryTreeNode | null
}

常见算法

梳理排序算法

冒泡排序（Bubble Sort）：

每次比较相邻的元素，如果顺序错误就交换它们，直到整个序列排序完成。
时间复杂度：平均情况和最坏情况下为 O(n^2)，最好情况下为 O(n)（当输入已经有序时）。
空间复杂度：O(1)。
稳定性：稳定排序算法。
实现方法: 双重遍历，相邻比较，前面的比后面的大就交换位置。

function modifiedBubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    let curNum = arr.length - 1 - i
    for (let j = 0; j < curNum; j++) {
      if (arr[j] > arr[j + 1]) {
        ;[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]
      }
    }
  }
  return arr
}

// 使用
const oldArr = [3, 4, 5, 1, 2, 7, 8]
console.log('🚀 ~ modifiedBubbleSort:', modifiedBubbleSort(oldArr))

插入排序（Insertion Sort）：

将数组分为已排序和未排序两部分，每次从未排序部分取一个元素插入到已排序部分的正确位置。
时间复杂度：平均情况和最坏情况下为 O(n^2)，最好情况下为 O(n)（当输入已经有序时）。
空间复杂度：O(1)。
稳定性：稳定排序算法。
实现方法: 从前向后排，前面的已经拍好序了，只需要将后面的插入到前面的正确位置。

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    const insertItem = arr[i] // 当前要插入的值, 临时存储

    let j = i // 从后往前开始遍历的初始序号(前面已经排好序了)
    while (j > 0 && arr[j - 1] > insertItem) {
      arr[j] = arr[j - 1]
      j--
    }
    arr[j] = insertItem
  }
  return arr
}

const oldArr = [3, 4, 5, 1, 2, 7, 8]
console.log('🚀 ~ insertionSort:', insertionSort(oldArr))

选择排序（Selection Sort）：

每次从未排序部分选择最小（或最大）的元素，放到已排序部分的末尾。
时间复杂度：平均情况和最坏情况下为 O(n^2)，不论输入的初始状态如何。
空间复杂度：O(1)。
稳定性：不稳定排序算法。
实现方法：从前往后，依次寻找当前最小值，并插入到最小值的位置。

/** 从前往后, 依次寻找当前最小值 */
function selectionSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    let indexMin = i // 当前最小值下标
    let curIndex = i + 1
    // 依次遍历, 找到最小下标
    while (curIndex < arr.length) {
      if (arr[indexMin] > arr[curIndex]) {
        indexMin = curIndex
      }
      curIndex++
    }
    // 最小下标发生变化
    if (indexMin !== i) {
      ;[arr[i], arr[indexMin]] = [arr[indexMin], arr[i]]
    }

    return arr
  }
}

const oldArr = [3, 4, 5, 1, 2, 7, 8]
console.log('🚀 ~ selectionSort:', selectionSort(oldArr))

希尔排序（Shell Sort）:
- 希尔排序是选择排序的一种改良，也被称为缩小增量排序。它通过将待排序的序列分割成多个子序列来进行排序，最终逐步缩小增量，直至整个序列有序。
- 排序步骤：
  - 选择增量序列: 选择一种初始增量序列，常见的是希尔增量序列（N/2、N/4、N/8...）
  - 按增量进行插入排序：从第一个开始以增量序列为间距，数字俩俩比较排序；排序完毕后缩小增量序列（如 N/2 --> N/4），继续插入排序，直至增量序列变为 1。
- 希尔排序的时间复杂度取决于增量序列的选择，最坏情况下为 O(n^2)，但在平均情况下，其性能通常较好。希尔排序是一种不稳定的排序算法。
快速排序（Quick Sort）：
- 选择一个基准元素，将序列分为小于等于基准和大于基准的两部分，然后对这两部分递归地进行快速排序。
- 时间复杂度：平均情况下为 O(nlogn)，最坏情况下为 O(n^2)（当输入已经有序时）。
- 空间复杂度：取决于递归调用栈的深度，平均情况下为 O(logn)，最坏情况下为 O(n)。
- 稳定性：不稳定排序算法。
归并排序（Merge Sort）：
- 将序列递归地分成两半，对每一半进行归并排序，然后将两个有序的半部分归并成一个有序的序列。具体步骤为:
  - 分割：将待排序的序列不断地二分，直到分割成单个元素的子序列（递归的基本情况）。
  - 合并：将两个有序的子序列合并成一个有序的序列。创建一个临时数组（或列表）来存储合并后的序列。比较两个子序列的首个元素，将较小（或较大）的元素放入临时数组，并将对应子序列的索引向后移动。
  - 重复上述步骤，直到一个子序列的所有元素都放入了临时数组。将另一个子序列中剩余的元素依次放入临时数组。将临时数组中的元素复制回原始序列的相应位置。
  - 递归：对分割后的子序列递归地应用上述步骤，直到所有子序列都排序完成。
- 时间复杂度：平均情况和最坏情况下为 O(nlogn)，不论输入的初始状态如何。
- 空间复杂度：取决于递归调用栈的深度，平均情况和最坏情况下为 O(n)。
- 稳定性：稳定排序算法。
堆排序（Heap Sort）
- 堆排序（Heap Sort）是一种利用堆数据结构进行排序的算法。堆是一种特殊的完全二叉树，具有以下性质：
  - 对于大顶堆（或大根堆），任意节点的值都大于（或等于）其子节点的值。
  - 对于小顶堆（或小根堆），任意节点的值都小于（或等于）其子节点的值。
提示
堆排序的基本思想是将待排序序列构建成一个堆，然后依次从堆顶取出最大（或最小）元素，放入已排序的部分，再调整堆，重复这个过程，直到整个序列排序完成。
下面是堆排序的基本步骤：
- 构建堆：将待排序序列构建成一个堆。
  - 从最后一个非叶子节点开始，向上遍历到根节点，对每个节点进行下沉操作，使其满足堆的性质。
  - 下沉操作：比较节点与其子节点的值，如果节点的值小于（或大于）子节点的值，则交换它们，并继续向下比较。
- 排序：重复以下步骤，直到堆为空。
  - 将堆顶元素（最大或最小元素）与堆的最后一个元素交换位置。
  - 将堆的大小减 1（即将最后一个元素从堆中移除）。
  - 对新的堆顶元素进行下沉操作，使其满足堆的性质。
堆排序的时间复杂度是 O(nlogn)，其中 n 是待排序序列的大小。构建堆的时间复杂度是 O(n)，排序的过程需要执行 n 次下沉操作，每次下沉的时间复杂度是 O(logn)。堆排序是一种不稳定的排序算法，因为在堆的调整过程中，元素的相对顺序可能发生改变。
堆排序的优点是原地排序（只需要常数级的额外空间），适用于大规模数据的排序。然而，由于堆排序的元素访问方式不连续，对于缓存性能较差的计算机体系结构，可能导致较高的缓存失效率。

Interview -- 算法

# 常见数据结构

# 栈 Stack

# 队列 Queue

# 链表 Linked list

# 树 Tree

# 二叉树

# 常见算法